Research.
Analog Machine Learning
Silicon brain: Pattern recognition and neurocomputing.
For decades, attempts have been made in the fields of artificial intelligence and computer science to reverse engineer the brain and the neural processes of memory, learning and adaptation.
Nanomechanical Computing
Logically reversible and irreversible computation.
Motivated by the challenge of energy-efficient computing with existing transistor-based technologies, we are focusing on an alternate architecture that uses nanomechanical resonators as building blocks of reversible and irreversible logic gates.
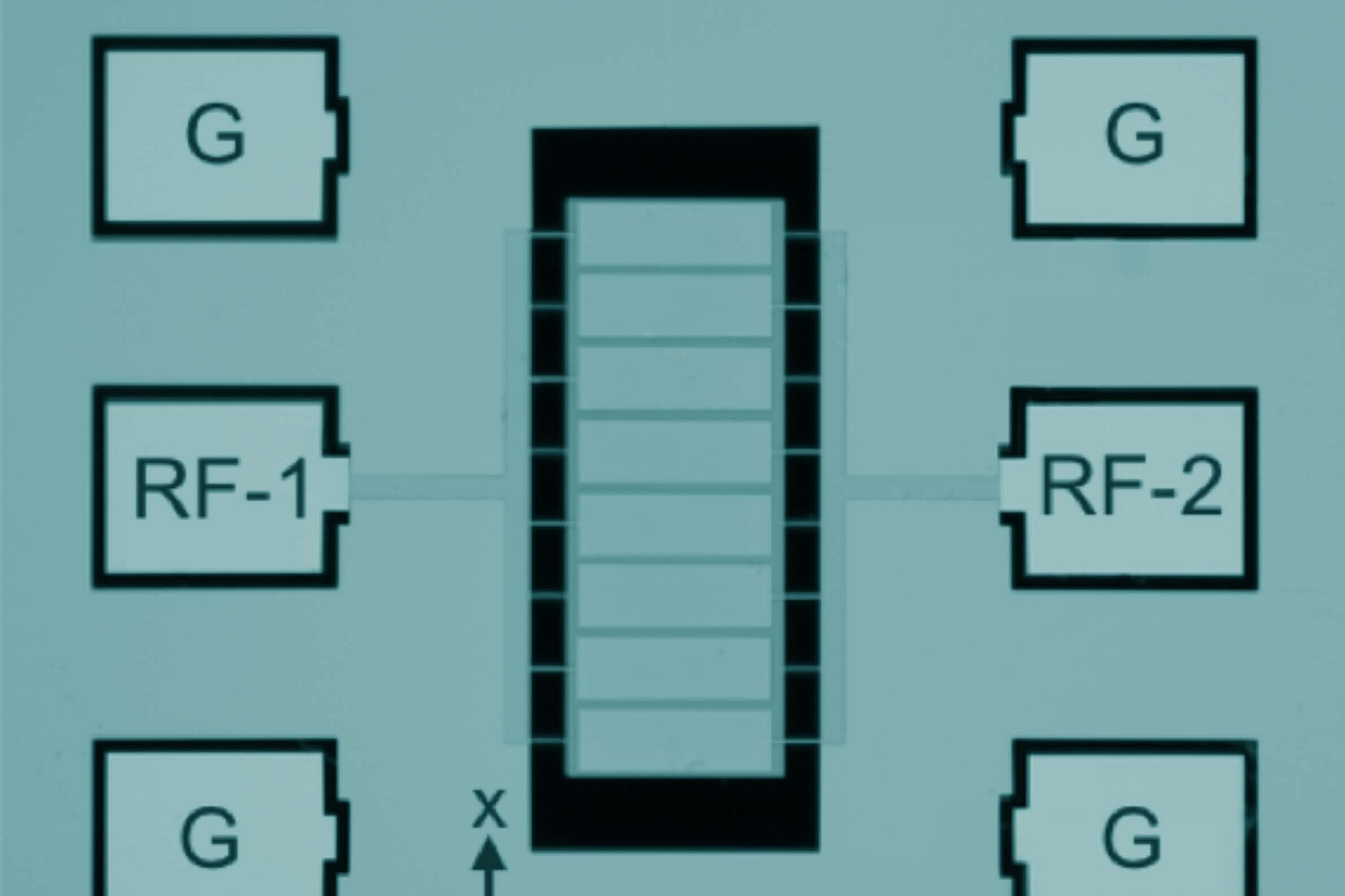
Wireless Power Transfer
Micro-scale wireless charging device as an implantable neuromodulator.
In 1914, Nikola Tesla was awarded a patent that described wireless power transfer (Apparatus for wireless transmission of electrical energy, US Patent 1,119,732).
Functional Nanomaterials
Using nanoscale devices to study material properties on nanoscale.
Nanomechanical measurement of spin dynamics can be done by detecting the corresponding change in angular momentum or torque.

Making small nano scale devices do amazingly big things.
An antenna design that taps into electric fields across air gaps makes low-power, wireless biomedical implants more feasible. Micromechanical resonators are tiny, silicon-based cantilevers that, due to their sensitivity to high-frequency AC fields, are being targeted as the receiving elements in wireless power designs.
Stochastic resonance is a counterintuitive concept: the addition of noise to a noisy system induces coherent amplification of its response.
Irreversible logic operations inevitably discard information, setting fundamental limitations on the flexibility and the efficiency of modern computation. To circumvent the limit imposed by the von Neumann–Landauer (VNL) principle, an important objective is the development of reversible logic gates, as proposed by Fredkin, Toffoli, Wilczek, Feynman, and others.
We present a nanomechanical device, operating as a reprogrammable logic gate, and performing fundamental logic functions such as AND/OR and NAND/NOR. The logic function can be programmed (e.g., from AND to OR) dynamically, by adjusting the resonator’s operating parameters.
We report the realization of a completely controllable high-speed nanomechanical memory element fabricated from single-crystal silicon wafers.
We demonstrate a silicon-based high-frequency nanomechanical device capable of switching controllably between two states at room temperature.
Radiation pressure exerted by light on any surface is the pressure generated by the momentum of impinging photons. The associated force – fundamentally, a quantum mechanical aspect of light – is usually too small to be useful, except in large-scale problems in astronomy and astrodynamics.
Coupling of nonlinear polarization in a dielectric medium in a piezoelectric film to mechanical motion leads to a resonator with nonlinear behavior in the acoustic frequency range.
Spin is an intrinsically quantum property, characterizing angular momentum. A change in the electron spin state is equivalent to a change in the angular momentum or mechanical torque. Could this torque be measured by nanomechanical torsion resonator?
Towards practical realization of brain-inspired computing in a scalable physical system, we investigate a network of coupled micromechanical oscillators.
We report measurements of synchronization in two nanomechanical beam oscillators coupled by a mechanical element. We charted multiple regions of frequency entrainment or synchronization by their corresponding Arnold’s tongue diagrams as the oscillator was driven at subharmonic and rational commensurate frequencies.
Diamond is amazing. It is an extremely hard material with high fracture constant and high elastic modulus. It conducts heat better than gold, copper and silicon. Naturally occurring diamond is an electrical insulator, however with suitable doping it can be easily transformed into a semiconductor or even a conventional superconductor with relatively high critical temperature.
Synchronized radiation from arrays of oscillators is widely used in microwave and wireless communications. Phase-locked oscillations produced at the atomic level now pave the way for devices on the nanoscale. Seen in southeast Asia, it is one of the most dazzling natural visual effects known: large congregations of fireflies blinking on and off in unison (Fig. 1).
Dissipation of energy in micro- and nano-electromechanical resonators governs their dynamical response and limits their potential use in device applications. Quantified by the quality factor Q, dissipation (1/Q) usually occurs by energy loss mechanisms that are linear, appearing as a damping term proportional to the velocity.
This article is a review of the dissipation processes in nanoelectromechanical systems (NEMS).
We report wireless actuation of a Lamb wave micromechanical resonator from a distance of over 1 m with an efficiency of over 15%.
Wireless transfer of power via high frequency microwave radiation using a miniature split ring resonator rectenna is reported. The near-field behavior of the rectenna is investigated with microwave radiation in the frequency range between 20-40 GHz with a maximum power level of 17 dBm.
The first microphone was invented and patented by Emile Berliner in the late nineteenth century. Since then, microphone diaphragm sizes have shrunken to as- tounding sizes and continue to shrink.
Wireless transfer of information is the basis of modern communication. It includes cellular, WiFi, Bluetooth, and GPS systems, all of which use electromagnetic radio waves with frequencies ranging from typically 100 MHz to a few GHz.
We present the effect of temperature on the switching characteristics of a bistable nonlinear nanomechanical beam.
We report direct measurements of average vibration energy in a high frequency flexural resonance mode achieved via an-harmonic elastic coupling to a fundamental vibration mode of a nanomechanical resonator.